Jet energy corrections and resolution

Overview

Teaching: 40 min
Exercises: 20 min

Questions

• What are jet energy correction?

• What is jet energy resolution?

Objectives

• Learn about how we calibrate jets in CMS.

• Learn about the resolution of the jets and its effect.

After following the instructions in the setup (if you have not done it yet) :

cd <YOUR WORKING DIRECTORY>/notebooks/DAS/
source /cvmfs/sft.cern.ch/lcg/views/LCG_104/x86_64-centos7-gcc11-opt/setup.sh
jupyter notebook --no-browser --port=8888 --ip 127.0.0.1

This will open a jupyter notebook tree with various notebooks.

Jet Energy Corrections

Let’s define the jet pt response $R$ as the ratio between the measured and the true pt of a jet from simulation. We expect that the average response is different from 1 because of pileup adding energy or non-linear calorimeter response.

Jet energy corrections (JEC) corrects reconstructed jets (on average) back to particle level. This is done against many useful metrics, like $p_T^{gen}$, $\eta$, area, pileup. CMS uses a factorized approach to JECs:

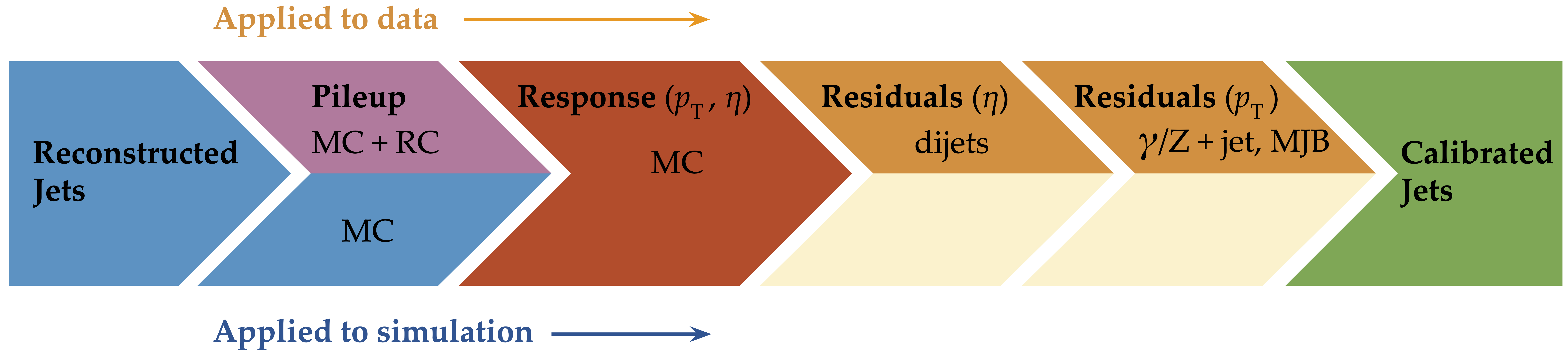
• Pileup corrections to correct for offset energy (noPU vs. PU jet matching). This is usually called L1FastJet.
• Correction to particle level jet vs. 𝑝𝑇 and η from simulation. This is called L2Relative and L3Absolute, or L2L3 together.
• Only for data: Small residual corrections (Pileup/relative and absolute) to correct for differences between data and simulation. This is called L2L3Residuals.

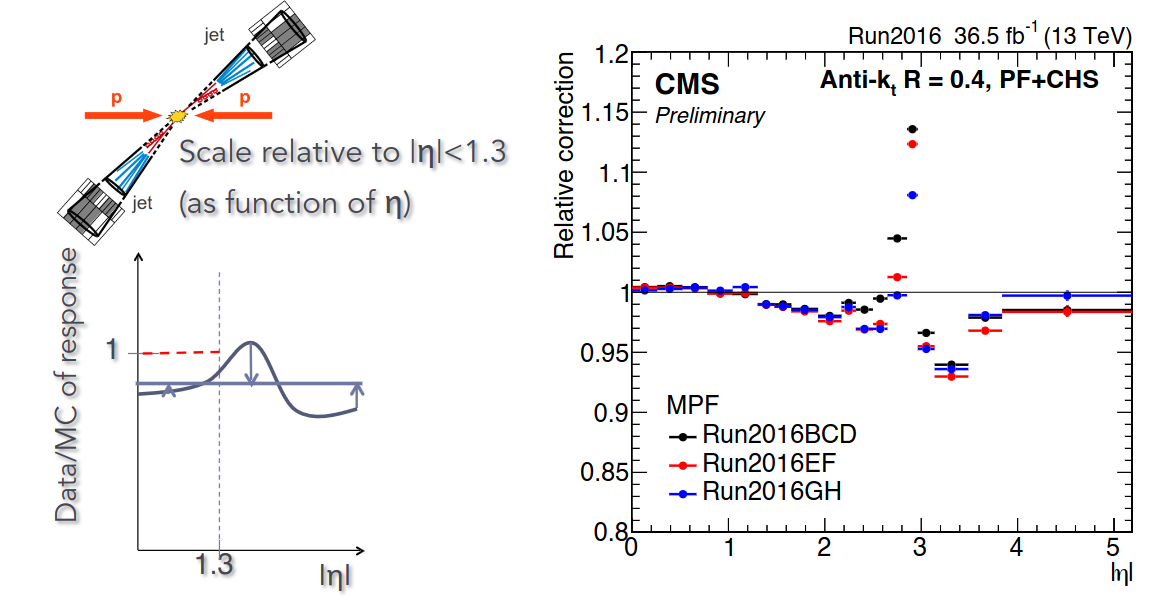
Jet energy scale determination in data

Reminder for PUPPI jets

PUPPI jets do not need the L1 Pileup corrections. Starting Run3, PUPPI jets are the primary jet collection.

Exercise 3.1

Open a notebook

For this part open the notebook called Jet_Energy_Corrections.ipynb and run the Exercise 3.1

Discussion 1.1

After running Exercise 1 of the notebook, were you expecting differences between these two distributions? Do you think the differences are large or small?

After running the Exercise 1 of the notebook, we can notice that the $p_{\mathrm{T}}$ distributions disagree quite a bit between the GenJets and PFJets. We need to apply the jet energy corrections (JECs), a sequence of corrections that address non-uniform responses in $p_{\mathrm{T}}$ and $\eta$, as well as an average correction for pileup. The JECs are often updated fairly late in the analysis cycle, simply due to the fact that the JEC experts start deriving the JECs at the same time the analyzers start developing their analyses. For this reason, it is imperative for analyzers to maintain flexibility in the JEC, and the software reflects this.

For more information and technical details on the jet energy scale calibration in CMS, look at the following link: https://cms-jerc.web.cern.ch/JEC/.

It is possible to run the JEC software “on the fly” after you’ve done your heavy processing (Ntuple creation, skimming, etc). We will now show one example on how this is done using the latest correctionlib package and the JME json-pog in the Exercise 2.

json-pog and correctionlib

Currently CMS and the jetMET POG is supporting the use of the so-called json-pog with the correctionlib python package, in a way to make the implementation of corrections more uniform.

Specifically JECs were delivered in the past in a zip file containing txt files where the users could find the corrections. The json-pog makes this process more generic between CMS POGs, and the correctionlib makes the implementation of this corrections also more generic.

More about json-pog in this link and correctionlib in this link.

In the notebook, using the json-pog and the correctionlib package, you find the following lines:

jerc_file = '/cvmfs/cms.cern.ch/rsync/cms-nanoAOD/jsonpog-integration/POG/JME/2018_UL/jet_jerc.json.gz'
jerc_corr = correctionlib.CorrectionSet.from_file(jerc_file)

corr = jerc_corr.compound["Summer19UL18_V5_MC_L1L2L3Res_AK4PFchs"]

where the string Summer19UL18_V5_MC_L1L2L3Res_AK4PFchs contains the jetMET nomenclature for labeling the JECs. In this example:

• Summer19UL18_V5_MC corresponds to the JECs campaing; including data processing campaign, JEC version, and if is MC or DATA.
• L1L2L3Res is the JEC type. In this case corresponds to the set of L1FastJet, L2Relative, L2L3Residual, L3Absolute
• AK4PFchs is the type of jet: ak4 pfjet using CHS as a pileup removal algorithm.

Discussion 1.2

After running Exercise 2 of the notebook, how big is the difference in pt for corrected and uncorrected jets? Do you think it is larger at low or high pt?

Discussion 1.3

Why do we need to calibrate jet energy? Why is “jet response” not equal to 1? Can you think of a physics process in nature that can help us calibrate the jet response to 1?

Discussion 1.4

The amount of material in front of the CMS calorimeter varies by $\eta$. Therefore, the calorimeter response to jet is also a function of jet $\eta$. Can you think of a physics process in nature that can help us calibrate the jet response in $\eta$ to be uniform ?

JEC Uncertainties

Since we’ve applied the JEC corrections to the distributions, we should also assign a systematic uncertainty to the procedure. The procedure is explained in this link, and this is part of the Exercise 2.3 of the notebook.

Exercise 3.2

Open a notebook

For this part open the notebook called Jet_Energy_Corrections.ipynb and run the Exercise 3.

Question 1.1

After running the Exercise 3 of the notebook, does the result make sense? Is the nominal histogram always between the up and down variations, and should it be?

Jet Energy Resolution

Jets are stochastic objects. The content of jets fluctuates quite a lot, and the content also depends on what actually caused the jet (uds quarks, gluons, etc). In addition, there are experimental limitations to the measurement of jets. Both of these aspects limit the accuracy to which we can measure the 4-momentum of a jet. The way to quantify our accuracy of measuring jet energy is called the jet energy resolution (JER). If you have a group of single pions that have the same energy, the energy measured by CMS will not be exactly the same every time, but will typically follow a (roughly) Gaussian distribution with a mean and a width. The mean is corrected using the jet energy corrections. It is impossible to “correct” for all resolution effects on a jet-by-jet basis, although regression techniques can account for many effects.

As such, there will always be some experimental and theoretical uncertainty in the jet energy measurement, and this is seen as non-zero jet energy resolution. There is also other jet-related resolutions such as jet angular resolution and jet mass resolution, but JER is what we most often have to deal with. Jets measured from data have typically worse resolution than simulated jets. Because of this, it is important to ‘smear’ the MC jets with jet energy resolution (JER) scale factors, so that measured and simulated jets are on equal footing in analyses. We will demonstrate how to apply the JER scale factors, since that is applicable for all analyses that use jets.

More information can be found at theand jet resolution guide.

The resolution is measured in data for different eta bins, and was approximately 10% with a 10% uncertainty for 7 TeV and 8 TeV data. For precision, it is important to use the correctly measured resolutions, but a reasonable calculation is to assume a flat 10% uncertainty for simplicity.

Open a notebook

For this part open the notebook called Jet_Energy_Corrections.ipynb and run the Exercise 4.

In the notebook we will use the coffea implementation to apply JER to nanoAOD events. Notice that the function used to apply corrections will be updated soon to be compatible with json-pog.

Discussion

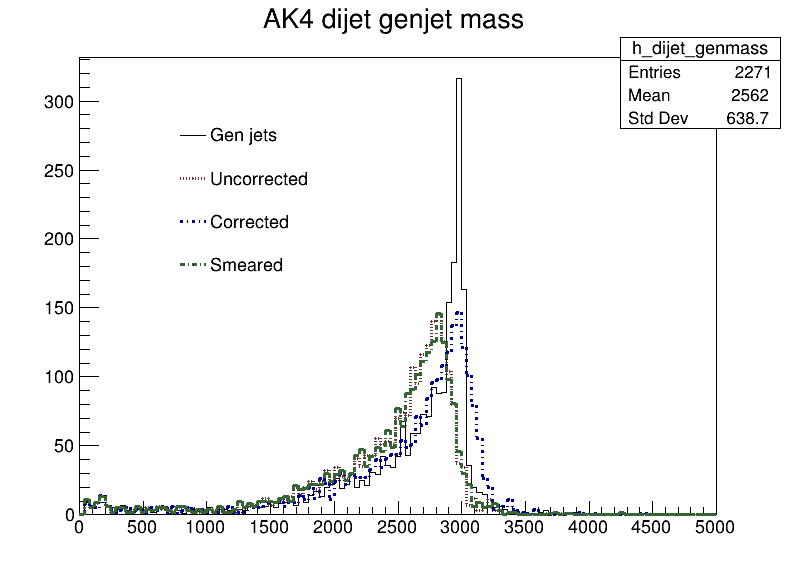
Let’s look at a simple dijet resonance peak shown below.

It corresponds to a dijet resonance peaks analysis. The plot was produced an MC sample of Randall-Sundrum gravitons (RSGs) with m=3 TeV decaying to two quarks. The resulting signature is two high-$p_{\mathrm{T}}$ jets, with a truth-level invariant mass of 3 TeV.

Can you see the effect the correction and the smearing has?

Key Points

• The energy of jets in data and simulations is different, for many reasons, and in CMS we calibrate them in a series of steps.

• Jets are stochastic objects which its content fluctuates a lot. We measure the jet energy resolution to mitigate this effects.